Programming Complex Dataflows in C

Over the past few months I’ve been spending a lot of time on implementing various signal processing algorithms in C/C++. Things like Kalman Filters, various types of FIR filters and finite state machines. The number of steps needed to implement each these algorithms were fairly small and in the beginning I tried to put all the functionality of these implementations into simple to use C++ classes. This made things look neater and also fit in quite well with the Arduino programming framework (I was implementing a lot of these algorithms on Arduino compatible microcontrollers like the Teensy). However, once I started combining different algorithms together to make something bigger, the code started becoming very messy. Making changes and debugging was starting to take longer and longer. In many instances, I had to go back and change the deisgn and interface of my C++ classes when I realized that the way I initially implemented it made it impossible or very difficult to do some step in the algorithm. I decided to take some time to figure out how I can do better. I wanted to find out a systematic method - a “meta-programming” algorithm if you will - that would tell me the way I should implement the algorithm so that the code is easy to write and more importantly, easy to read and debug.

Representing the Algorithm

Before I could start solving the problem I needed to decide how to represent a general data processing algorithm. What is a representation that can capture most if not all of the types of algorithms that I wanted to implement? I remembered that in a lot of papers that I’ve read, the authors used Simulink to implement their algorithm. So I decided to start out by assuming that I can represent what I want to do in the form of a block diagram - much like the block diagrams that you can draw in Simulink. It turns out that as long as they don’t have any cycles or loops, block diagrams with arrows representing the flow of data between the blocks can be represented by a mathematical structure called a Directed Acyclic Graph.

Directed Acyclic Graphs

Graphs as a mathematical structure (different from the graphs that you use to plot data) are useful for representing relationships between things. Intuitively I think of them as circles connected by lines. The circles represent things and the lines represent some type of relationship between the things. If this seems very abstract, that’s because graphs can be applied to a lot of different things and when an concept is that general, it tends to be very abstract. As an example, a graph can be used to represent an electrical circuit. Each discrete component like a resistor or an LED can be considered a node or vertex in the graph (circles). The wires that connect these components together can be considered the edges of the graph.

A directed graph is a graph in which the edges connecting the nodes have a direction. The graph in the image from xkcd is a directed graph since it has arrows connecting the nodes of the graph.

A directed acyclic graph (DAG) is a directed graph that does not have cycles in it. This means that there is no way to start at a node in the graph and follow the arrows from node to node and reach the node you started at. A directed acyclic graph is useful for modeling dependencies. If you’re planning to understand some big concept in science - General Relativitiy for example - there are prerequisite ideas that you need to understand first. A subject and it’s prerequisites can be arranged in the form of a directed acyclic graph.

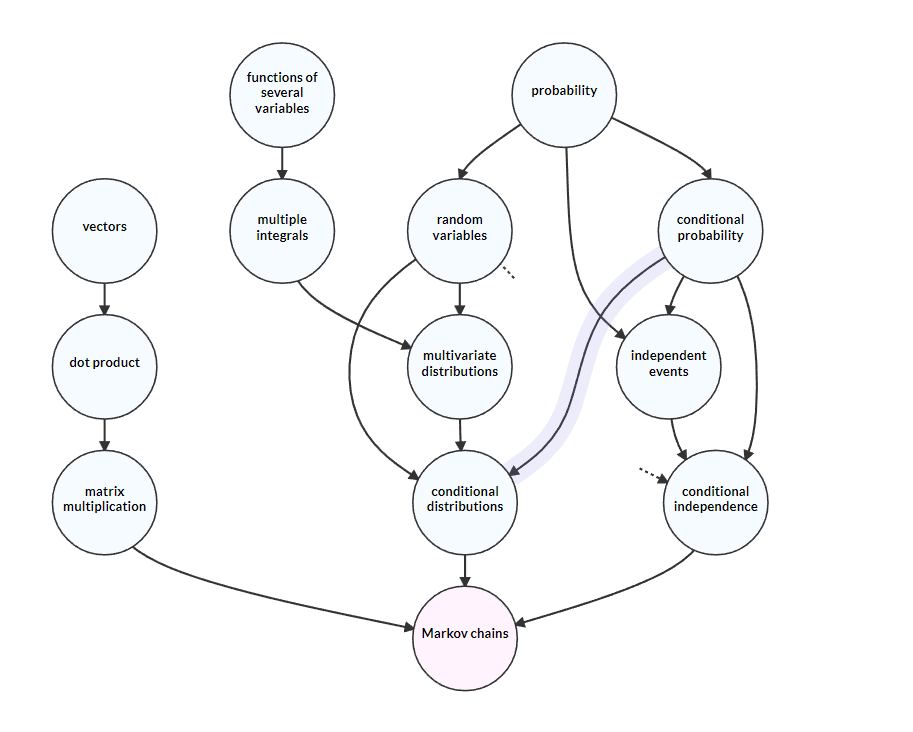
Topological Sorting

Given a DAG showing the dependencies for learning about Markov chains like in the image above, one might ask the question: Is there a way to list the nodes of the graph in correct learning order i.e the order in which any dependencies for a node appear before the node itself is listed. It turns out that you can! Every DAG has at least one way in which we can make this sorted list and there are a few algorithms for doing so.

So if you want to learn something new, topologically sorting a dependency graph of the topic is a nice approach! In fact, this is exactly what the website Metacademy does! It gives you the order in which to learn things using topological sorting.

Dataflows

So how does this relate to programming algorithms represented by block diagrams in C? I thought of the block diagram as a directed acyclic graph. The blocks which represent steps in the data processing algorithm are represented by nodes in the graph and the arrows that connect the blocks represent the flow of data. In programming, the nodes in the block diagram can be naturally represented by functions whose arguments are the incoming edges and the return values are the outgoing edges. This also means that the edges themselves can be naturally represented by variables in the C program. Once I’ve defined all the edge variables and block functions, I need to figure out what is the correct order in which to call each of these block functions. The “correct” order can be defined as the order in which each function is only called once all the variables that represent the input edges to the block have been updated (if necessary) in the current iteration of the main loop of the program. It turns out that this correct order is the same as the topologically sorted order of the function blocks.

So to summarize the systematic meta algorithm to implement a data processing algorithm in C:

Start out with a fresh .h file which will contain your implementation

1. Construct a block diagram of the algorithm showing the data flow.
2. Make sure that the block diagram is a directed acyclic graph.
3. Give names to each node and edge.
4. For each edge in the graph, declare a C variable in the global scope. I use the static keyword if I want to make sure that the variable is only visible inside the header file. The data type of the C variable depends on the node that the edge originates from.
5. For each node in the graph, declare a function that takes as arguments pointers to both the input and and output edge variables from the node. It is useful to declare the input pointers as const to ensure that the function does not modify the data in the edge variables. The function uses the input to carry out the processing step and modifies the output edge variables. I use static variables inside the function if I need to keep track of any state (like for finite state machines).
6. Any parameters needed by the processing step inside the function can either be declared globally or as a const argument of the function. Personally, I like to have the simple parameters as #defines at the top of the header file so I can tweak/change them easily.
7. If there are parameters that need to be modified/tuned during execution, they can be declared as variables global to the file. This is useful if you’re running a code that implements something like a PID controller and you want to tune the gains of the controller online. I use an Arduino library that listens to incoming commands on one of the Serial ports.
8. Define an initialization function that initializes all the edge variables to an initial state (if necessary).
9. Define a main function graph execution function that calls the block functions in the topologically sorted order.

Here’s a rough outline of what the .h file will look like.

#ifndef DATA_PROC_H
#define DATA_PROC_H

//#defines and parameters
#define PARAM1 0

//Define the edge variables with the appropriate type
float e1, e2, e3, e4
int e5;
//Define the node function prototypes
void F1(const float in1, const float in2, float *out);
void F2(const float in1, const float in2, float *out);
void F3(const float in1, int *out);

//Define the initialization function
void data_proc_init()
{
    e1 = 0;
    e2 = 0;
    e3 = 0;
    e4 = 0;
}

//Define the main execution pipeline function
void data_proc_exec()
{
    //Node functions called in the topologically sorted order
    F1(e1, e2, &e3);
    F2(e2, e3, &e4);
    F3(e4, &e5);
}

//Function implementations
//Implement the node functions here

#endif

And in the main C file:

#include "data_proc.h"

int main(int argc, char** argv)
{
    //Run the initialization function
    data_proc_init();

    while(loop_condition)
    {
        //Execute pipeline function in loop
        data_proc_exec();
    }
}

I’ve noticed that if I stick to these rules consistently, my code is generally much easier to read. As long as I give descriptive names to the block functions, I only need to look at the main execution function to figure out the flow of the program. Debugging becomes easier too! It becomes a matter of adding one function from the topologically sorted list at a time and checking the output for correctess.

While the meta algorithm that I wrote down is specifically for C, this method can easily be extended to other programming languages. Python would make doing this even easier as it is much more flexible with functions returning data. Instead of taking in pointers to the output variables as arguments, the function can actually return tuples of data that can be assigned to the output edge variables.

I’m sure that this method will have some limitations. One I can see right away is that it uses a lot of variables. One for each edge and even more for the static variables inside the function. On memory constrained systems like small microcontrollers, the RAM can run out pretty fast (Declaring non-tweakable parameters as being stored in the code ROM should help with this a bit). Another problem is the question of what to do with algorithms that can’t be represented as a DAG. I don’t know if it’s possible to represent all possible algorithms using DAGs (A quick google search did not turn up any conclusive answers). I am also unsure how this model can be used for programming things like GUIs which sit around and wait for events to happen most of the time. However, when implementing control and signal processing algorithms, I find this method is singularly better than the others I’ve tried.